Note

The latest example has been generated using MAG3D v6.0.2. The exercise can be completed using previous versions. However some functionality has been added since v5.0, and improvements in performance since v6.0 and v6.0.1 may result in slightly different recovered models.

5.5. Sparse Norm Inversion

Here, we use magsen3d_60.exe to compute the sensitivity matrix required for the inversion; which is scaled by distance weighting. We then use maginv3d_60.exe to invert the data using sparse norms to recover a model compact susceptibility model. To keep the example simple, we added Gaussian noise with a standard deviation of 0.5 nT to all data points. We then assigned uncertainties of 0.5 nT to all magnetic data. In practice, the noise on the data is not trivial to quantify and choosing appropriate uncertainties is very important for successful inversion.

Files relevant to this part of the example are in the sub-folder inv_sparse . Before running this example, you may want to do the following:

• Download and open the zip folder containing the entire Mag3d example (if not done already)

• Learn how to run magsen3d_60.exe and maginv3d_60.exe from the command line

• Learn the format of the input file for magsen3d_60.exe and of the input file for maginv3d_60.exe

5.5.1. Sensitivities

Note

If using MAG3D v6.0.2, the last line in the input file is unused and the sensitivity matrix can be used for the L2 inversion can be reused for sparse-norm inversion.

Note

If using MAG3D v6.0.2, a larger value of eps (e.g. 0.05) can generally be used for the wavelet compression. That is because the wavelet compression is acting on sensitivities after distance weighting has been applied, not before

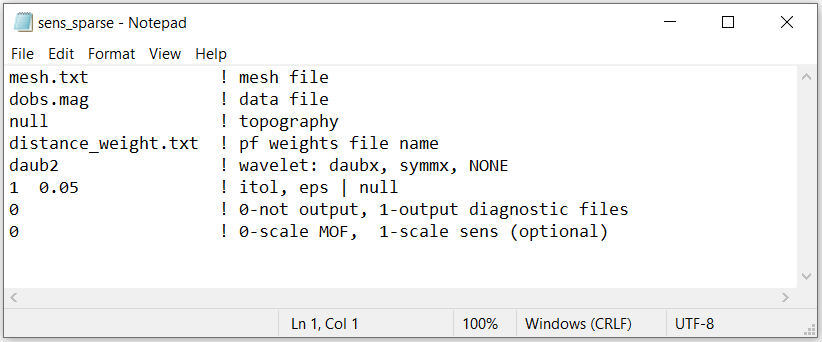
Here, the code magsen3d_60.exe and the input file sens.inp (see format ) are used to construct the sensitivity matrix and scale it using distance weighting. The distance weighting is applied to the sensitivity matrix to counteract the inversion’s natural tendancy to incorrectly place anomalous structures near the observation locations.

To compute the sensitivities, the following input file was used. Since we are no longer performed an least-squares inversion, a flag of 0 must be entered on the last line of the input file.

5.5.2. Inversion

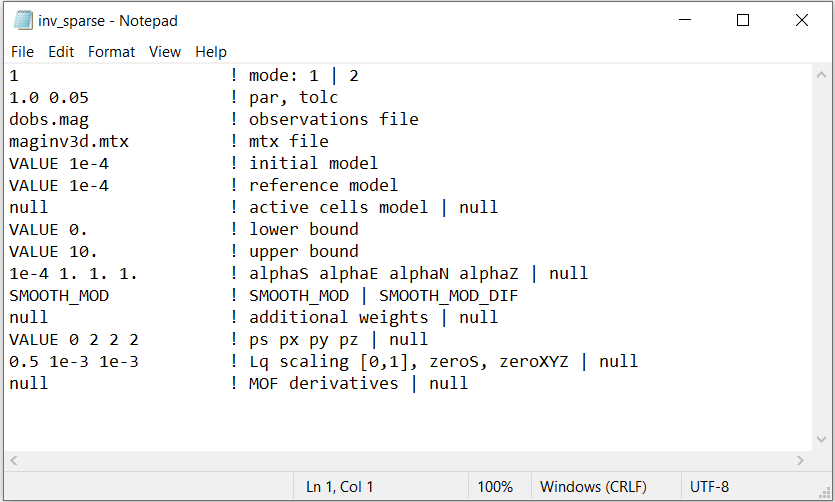
Here, the code maginv3d_60.exe and the input file inv.inp (see format ) was used to recover a susceptibility model. You cannot perform the inversion until you have created the sensitivity matrix. For this example, we set P=0 and Qx=Qy=Qz=2. That is, we would like to recover a model that is compact but still smooth. To see how these parameters impact the recovered model, see the GIFtools cookbook .

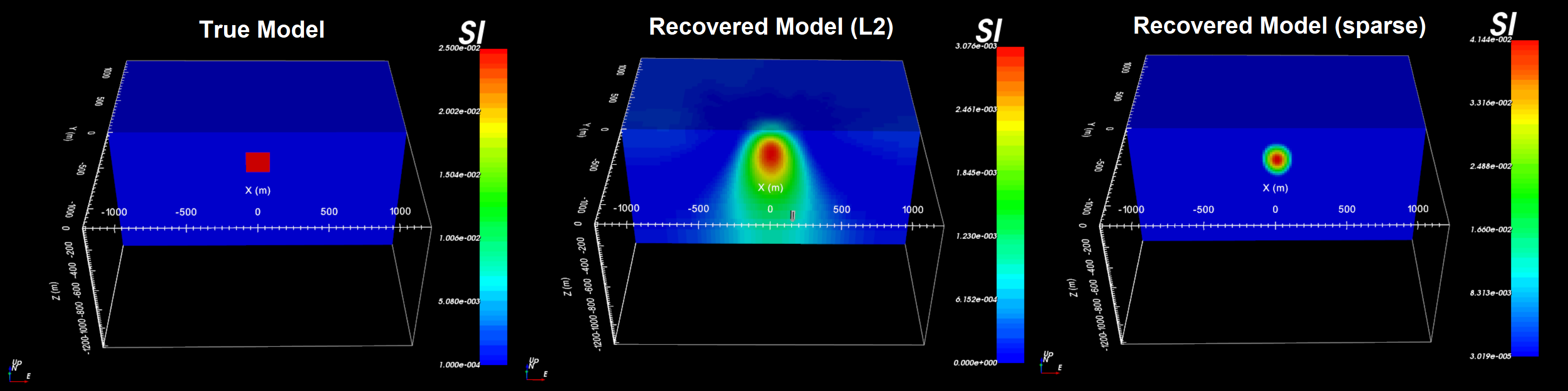
The true model (left), recovered model using least-squares (middle) and recovered model using sparse norms (right) are shown below. Unlike the least-squares result, the sparse norm result is a compact structure whose maximum amplitude is much closer to that of the true model. And the distance weighting is able to place the center of the recovered model at the correct depth.